Este pequeño ejercicio matemático está destinado a todos aquellos que consideran que la Argentina es un país “en serio”.
Estas son las conclusiones del estudio del Contador Morra:
“1935-2005: 70 años y una pequeña Historia de Incompetencia sin Igual”.
En el año 1935, con 3,90 pesos moneda nacional (m$n) se podía comprar un dólar estadounidense. (3,90 m$n = 1 U$S). A principios del año 2005 se deben tener 3,00 pesos ($) para comprar 1 U$S.
En una lectura rápida y sin prestar mucha atención, algún distraído podría concluir:
“Qué bien que se ve: hubo estabilidad durante 70 años y nuestra moneda mejoró su cotización con respecto a la divisa extranjera, indicando una mayor solvencia y un mejor desarrollo de Argentina como país, con relación a Estados Unidos de Norteamérica”.
La estabilidad de la moneda tiene una influencia muy importante en el desarrollo de cualquier sociedad organizada, y su valor con relación a otras divisas y con los bienes susceptibles de intercambio, depende fundamentalmente de la confianza que generan aquellas personas que tienen capacidad de decisión en la estrategia política de un país.
Sin embargo, la historia dice que con el paso del tiempo, a la moneda nacional hubo que agregarle trece ceros hasta llegar al peso de hoy, de acuerdo al siguiente esquema:
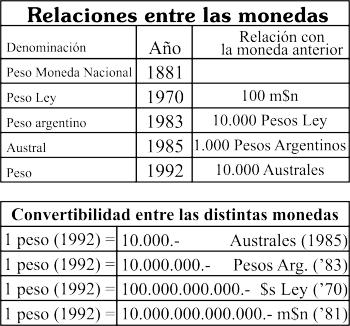Es interesante, en este caso, hacer un pequeño ejercicio matemático.
Si estuviera vigente aún el signo monetario de aquel momento, el peso moneda nacional (m$n), necesitaríamos 30.000.000.000.000 ó 30 billones ó 30 millones de millones de billetes de un peso moneda nacional para comprar un dólar. Cada fajo de 100 billetes tendría un valor de m$n 100, por lo que serían necesarios 300.000.000.000 de fajos.
Los billetes actuales son más chicos que los de aquella época, ya que tienen un tamaño uniforme de 155 mm. de ancho y 65 mm. de alto, pero, a los efectos de este cálculo, podemos tomarlo como ejemplo. El papel utilizado es 100 % fibra de algodón, con un peso de 83 gr/m2. (según el Banco Central de la República Argentina)
Cada fajo de 100 billetes tiene 1,0075 metros cuadrados de papel (0,155 * 0,065 *100), que se puede redondear en 100 billetes = 1 fajo = 1 m2.
Si cada fajo tiene 1 metro cuadrado y lo extendiéramos en el suelo, necesitaríamos 300.000.000.000 de metros cuadrados o su equivalente en kilómetros cuadrados: (1 km2 = 1.000.000 de m2 - 300.000.000.000 / 1.000.000)= 300.000 Km2.
La provincia de Santa Fe tiene una superficie de 133.007 km2 y la de Córdoba 165.321 km2, por lo tanto, entre las dos suman 298.328 Km2
Dos provincias cubiertas de billetes para comprar un solo dólar (1 U$S).
Si hacemos un cálculo sobre su peso, a ochenta y tres gramos el metro cuadrado o el fajo de 100 billetes tendríamos: 300.000.000.000 (fajos o m2) x 83 gramos (c/u), dividido 1.000 para transformarlos en kg y el resultado dividido 1.000 para transformarlo en toneladas, obtendríamos una cifra de: 24.900.000 toneladas.
Si tenemos en cuenta que un camión puede llevar 30 toneladas, tendríamos que tener 830.000 camiones llenos de billetes. Para hacer una comparación, la cosecha de soja del año 2004 fue de 39.000.000 de toneladas, por lo que el 64 % del peso de la cosecha de soja del tercer productor mundial, serían necesarios en billetes para comprar un solo dólar (1 U$S). Sin ningún elemento devastador de por medio (guerras, epidemias, meteoros, etc), con las condiciones naturales y poblacionales absolutamente favorables, fue realmente necesario un inmenso esfuerzo de parte nuestros beneméritos dirigentes de los últimos 70 años para lograr algo así” Θ
Lugar de residencia: 
Lugar de residencia: 
Ingredientes 
La cúrcuma o turmeric, a veces llamada azafrán indio o especia dorada, es una planta alta que crece en Asia y América Central.
Hola, amigos boxadictos, tal vez recuerdan mi nota publicada en el mes de marzo del año pasado en El Suplemento, donde se anunció la pelea del nuevo campeón latino super pluma de la Federación Internacional de Boxeo (FIB), el argentino Neri “El Maldito” Romero,
El gato colocolo, gato del pajonal o gato montés (Leopardus colocolo) es un mamífero de la familia Felidae.
Hubo un tiempo en el que toda la Sierra del Pillahuincó estuvo habitada por innumerables tribus Pampas.
Sin lugar a dudas, el baile del gato ocupa el primer lugar con una gran popularidad dentro del gauchaje.
Provincia de Mendoza
Por siempre el principal destino veraniego de los argentinos
Disneyland invita a todos los chicos a jugar con Lightning McQueen y Mater en Cars Land, un territorio repleto de diversión a toda máquina en el Disneyland Resort.
Entre los numerosos lugares turísticos en el área de Los Angeles, California, se encuentra Zuma Beach,
“Ese amor que nos negamos” 
Amor y terror en el Medio Oriente - Quinta edición
